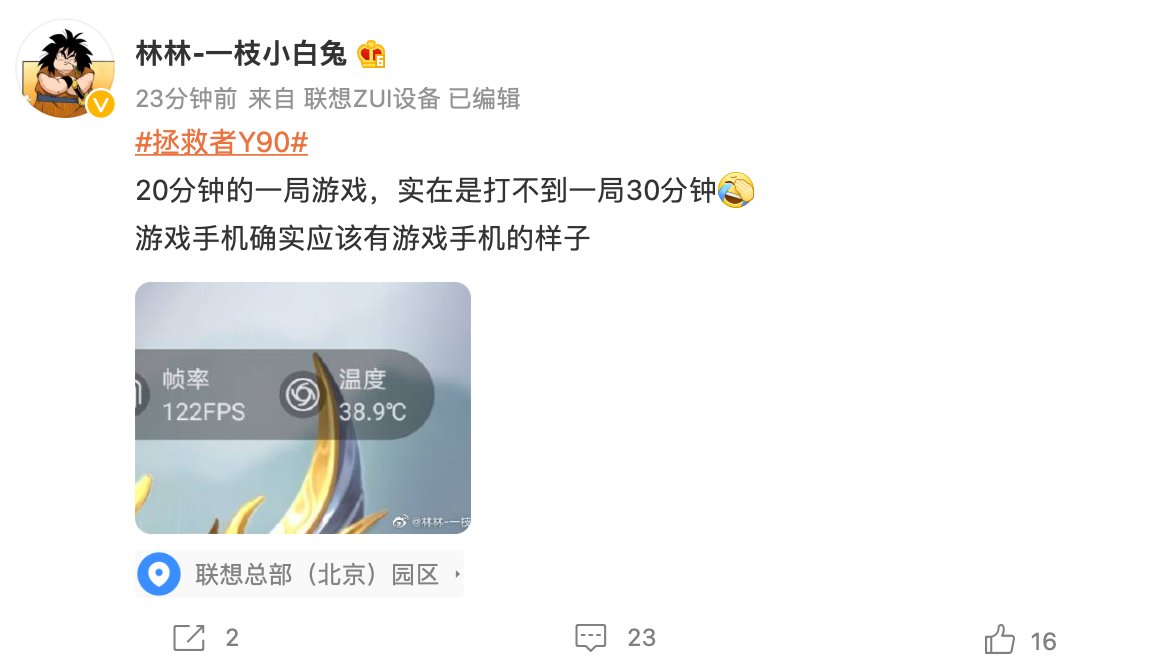
经验风险、期望风险、结构风险经验风险、期望风险、结构风

序
本次记录内容包括机器学习中的三种类型的风险函数
风险函数与损失函数的关系
统计学习模型旨在假设空间中寻找最佳的模型，那么需要指定一个准则来作为模型选取的评判标准。
因此引入了损失函数和风险函数。

损失函数：度量模型一次预测的好坏
风险函数：度量平均意义下的模型预测好坏

由损失函数推向风险函数
【经验风险、期望风险、结构风险】常见的损失函数：

文章图片

确定了损失函数后，那么自然地损失函数越小越好，由于模型的输入X，输出Y 是随机变量，遵循联合分布P(X, Y)，所以损失函数的期望为：

文章图片

（连续变量求积分，离散变量求和）
为什么要引入损失函数的期望呢？

原因是:人们希望模型能够刻画在全体样本上的预测能力！

解释：就目前为止，我们手头上的数据仅仅是训练集，想要刻画模型对训练集拟合的好坏，直接将单点误差损失相加求均值即可，但是我们的模型再怎样对训练集拟合的好，都无济于事，因为我们更多考虑的是模型对未知数据的拟合能力。那么如何衡量模型在全体数据集上的性能呢？自然而然，引入概率论中两随机变量的期望。
区别一下期望和均值：

文章图片

如果我们能进行无穷次随机实验并计算出其样本的平均数的话，那么这个平均数其实就是期望。当然实际上根本不可能进行无穷次实验，但是实验样本的平均数会随着实验样本的增多越来越接近期望，就像频率随着实验样本的增多会越来越接近概率一样
如果说概率是频率随样本趋于无穷的极限
那么期望就是平均数随样本趋于无穷的极限

经验风险与期望风险
我们将上面提到的训练集的总损失定义为经验风险，如下所示：

文章图片

将损失的期望称为期望风险，如下所示：

文章图片
怎样求风险？
机器学习问题求的是条件概率，那么有人就说了，既然上面提到了两随机变量的联合分布，那么我们根据条件概率-联合概率-边缘概率的关系岂不是可以直接求解？
其实，我们手头无法得到全体样本，因此，联合概率 P(X, Y) 是无法得到的，但是根据弱大数定律，当样本N无限大时，可用经验风险作为期望风险的估计，也就是局部估计整体。
那么我们常说的风险最小化其实就指的是经验风险最小化！
为何引入结构化风险？
虽然可以使用经验损失近似估计期望风险，但是大数定理的前提是N无穷大，实际上，我们的训练集一般不会特别大，此时就需要对经验风险做出适当调整才能近似估计。因此引入结构风险。
结构化风险是为了缓解数据集过小而导致的过拟合现象，其等价于正则化，本质上反应的是模型的复杂度。认为经验风险越小，参数越多，模型越复杂，因此引入对模型复杂度的惩罚机制。定义如下：

文章图片
正则化被定义为模型复杂度的单调函数，λ用于权衡经验风险与模型复杂度。
至此，我们认为结构风险最小化的模型是最优模型，因此，我们的优化问题变为：

文章图片
结构化风险本质
结构化风险（正则项）其实是加入了模型参数分布的先验知识，也就是贝叶斯学派为了将模型往人们期望的地方去发展，继而加入了先验分布，由于是人为的先验，因此也就是一个规则项（这也就是正则项名称的由来）。这样一来，风险函数将进一步考虑了被估计量的先验概率分布。
李航老师书中的两个疑惑