导数的应用

2021-09-21

一，利用导数求函数的单调性

导数与函数单调性的关系

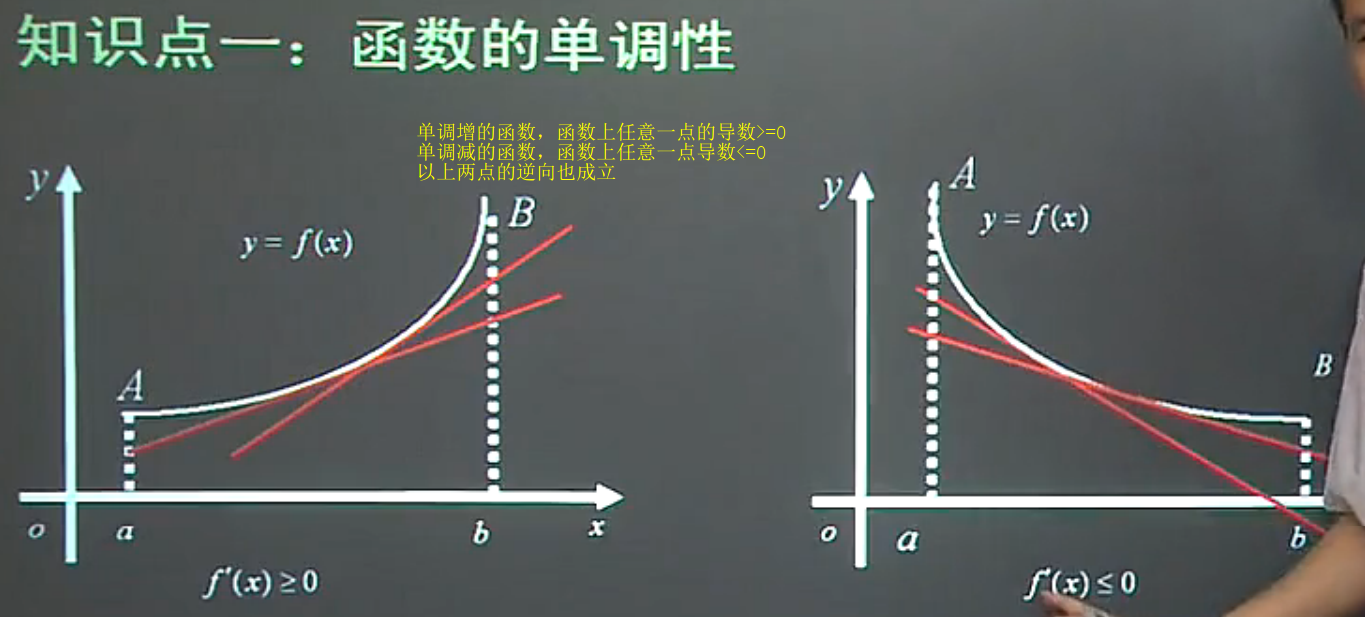
$导数的应用$
文章图片

$导数的应用$
文章图片

用导数求函数单调性的步骤

$导数的应用$
文章图片

举例

$导数的应用$
文章图片

$导数的应用$
文章图片

$导数的应用$
文章图片

应用单调性进行证明

$导数的应用$
文章图片

$导数的应用$
文章图片

二，极值定理

极大值：函数在x0某一个邻域左侧单调递增（左导数>0）,右侧单调递减（右导数<0），x0为极大值点；
极小值：函数在x0某一个邻域左侧单调递减（左导数<0）,右侧单调递增（右导数>0），x0为极小值点；

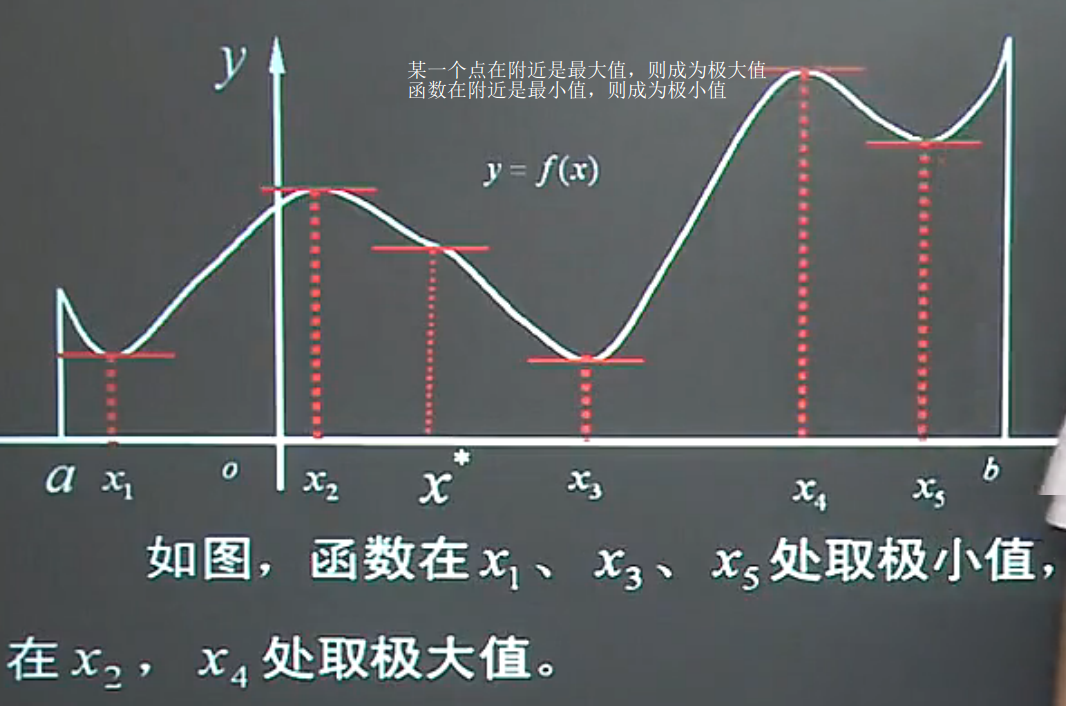
$导数的应用$
文章图片

$导数的应用$
文章图片

求函数极值点的方法一：一阶导数法

$导数的应用$
文章图片

$导数的应用$
文章图片

求函数极值点的方法二：二阶导数法, 注意是在驻点的基础上求二阶导数

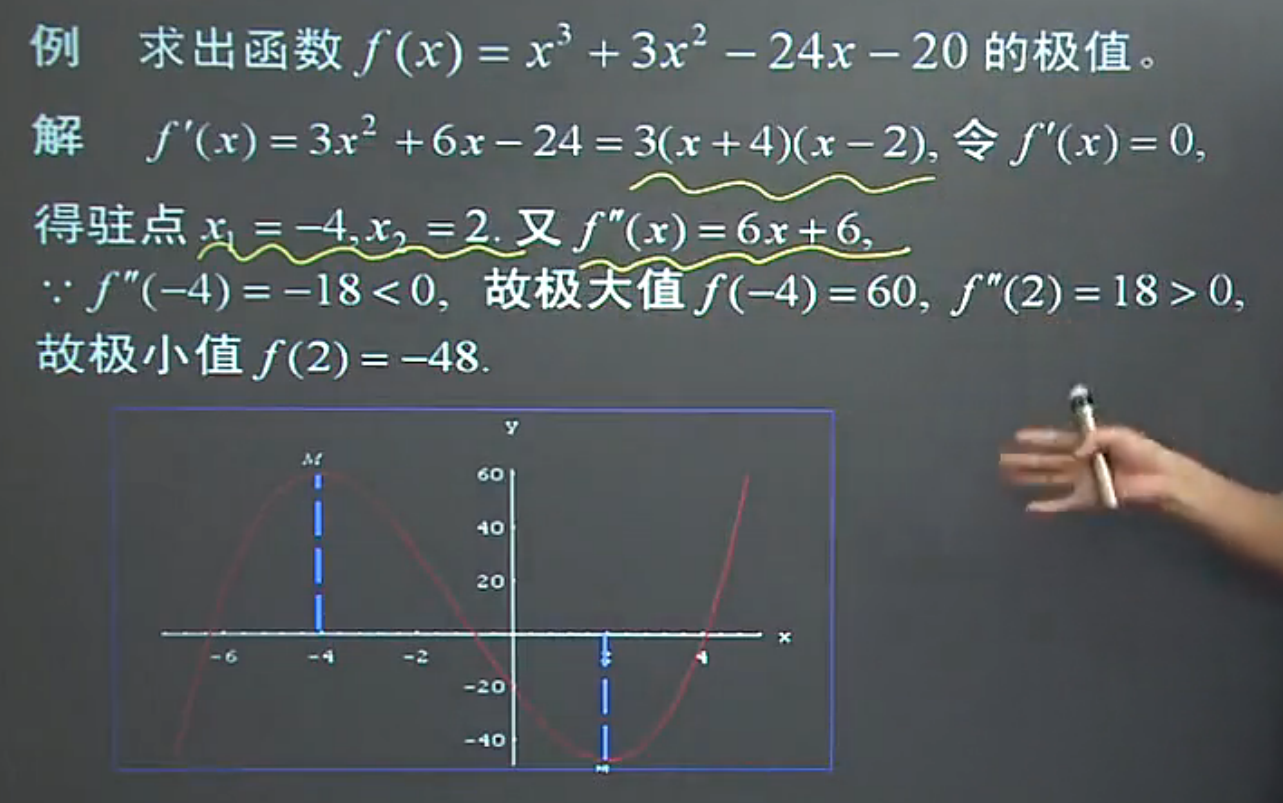
$导数的应用$
文章图片

$导数的应用$
文章图片

尽量使用方法二求极值，但是如果如果使用方法二极值不存在，那么就要使用第一种方法继续求：

$导数的应用$
文章图片

$导数的应用$
文章图片

三、函数的最值

1. 函数在给定区间内的最大值和最小值求法

$导数的应用$
文章图片

1. 函数的可能的最值点可能是　驻点（函数的导数＝０的点）或导数不存在（使导数无意义的点）或　函数两个端点　其中的一点；

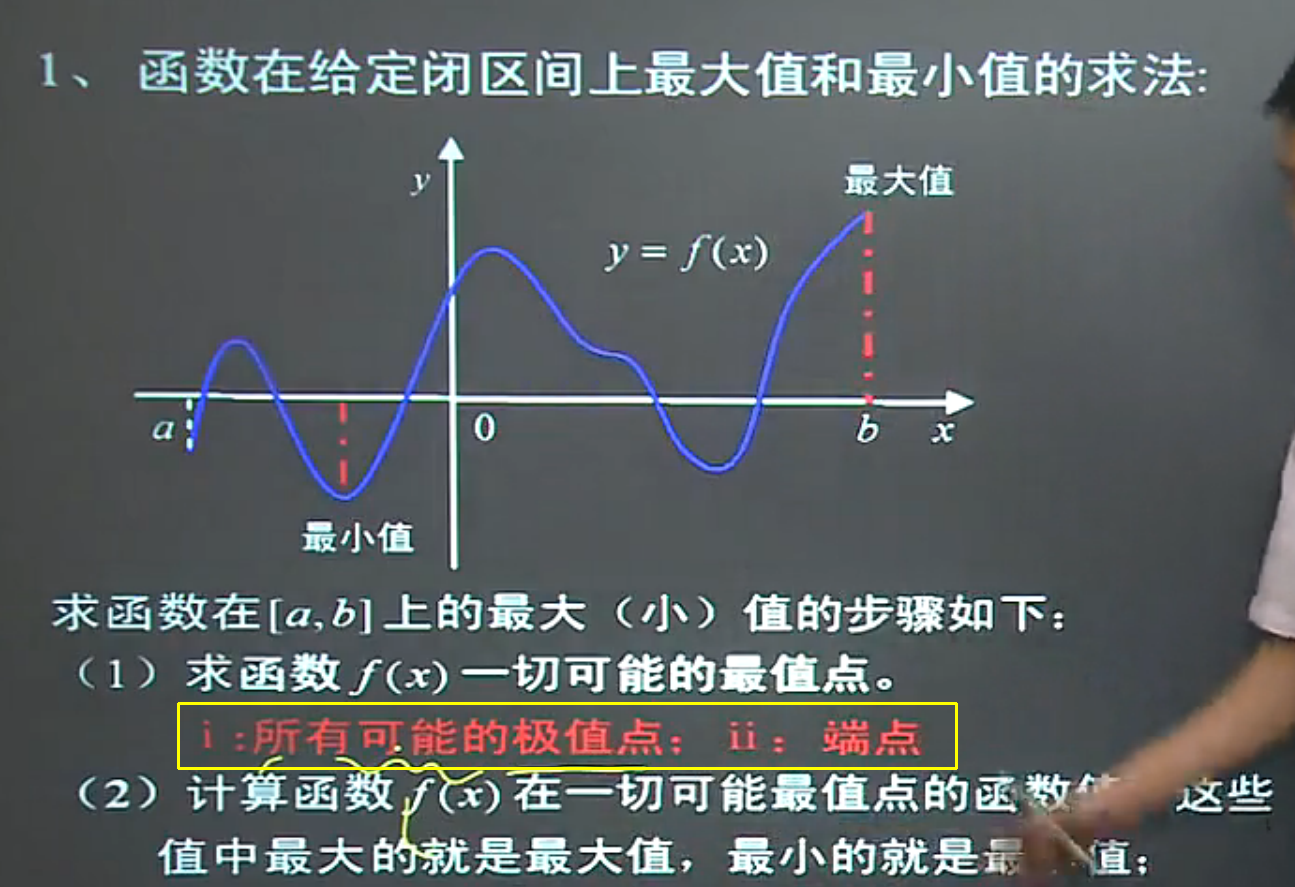
$导数的应用$
文章图片

$导数的应用$
文章图片

上图中的最值点就是驻点，使导数不存在的点不存在；

1. 实际问题的最值就是极值；

$导数的应用$
文章图片

$导数的应用$
文章图片

$导数的应用$
文章图片

$导数的应用$
文章图片

四、曲线的凸凹性

1. 定义

$导数的应用$
文章图片

1. 凹凸型的判定

$导数的应用$
文章图片

3.　函数曲线拐点的判定

$导数的应用$
文章图片

$导数的应用$
文章图片

$导数的应用$
文章图片

$导数的应用$
文章图片

四、曲线的渐进线, 水平渐进线用极限求，铅直渐进线是使得函数分母趋向于０，分子不为０的点求；

1. 水平渐进线

$导数的应用$
文章图片

1. 铅直渐进线

$导数的应用$
文章图片

【导数的应用】 $导数的应用$
文章图片

推荐阅读

上一篇：日照金色雨林丨这些秘诀，教您养出自律的孩子

下一篇：天赐良机，夏季排毒（四）