
文章图片
学习DIP第55天
转载请标明本文出处:***http://blog.csdn.net/tonyshengtan ***,出于尊重文章作者的劳动,转载请标明出处!文章代码已托管,欢迎共同开发:https://github.com/Tony-Tan/DIPpro
更多图像处理机器学习内容请访问最新网站www.tony4ai.com
#开篇废话
废话开始,今天介绍OTSU算法,本算法比前面给出的算法更能够给出数学上的最佳阈值,不需要任何输入附加参数、与同样不需要输入附加参数的迭代均值和均值阈值来比较,OTSU给出的阈值能使分类更加均匀。
阈值处理将灰度值分为两类,而对于分类问题,已有的一种最优闭合解–贝叶斯决策规则。
#贝叶斯决策规则
首先介绍下贝叶斯公式的形象化理解,考虑下图

文章图片
上面的12幅图中有手枪和弹夹,只有弹夹和手枪出现在同一个盒子的时候才有杀伤力,也就是你拿到一个盒子,你不知道里面是什么,有可能是枪,有可能是弹夹,有可能同时有枪和弹夹。下面来从概率学角度分析
设盒子里有枪为事件A,那么A出现的概率设为 p ( A ) p(A) p(A)。
设盒子里有弹夹为事件B,那么B出现的概率设为 p ( B ) p(B) p(B)。
那么同时出现事件A和事件B的概率为 p ( A B ) p(AB) p(AB)
看图可以知道
$p(A)=\frac{8}{12}=\frac{2}{3} $..........(1) $p(B)=\frac{7}{12} $..........(2) $p(AB)=\frac{3}{12}=\frac{1}{4} $..........(3) 考虑我们随机抽出一个盒子,先拿出一个东西,比如先拿出一把枪,那么也就是事件A发生了,那么我们继续从盒子里拿东西,有可能拿到弹夹,也有可能啥也没有,那么拿到弹夹的概率就如下:
$p(B|A)=\frac{3}{8} $..........(4) 同理,如果先拿出来的是个弹夹,那么接下来拿出枪的概率是:
$p(A|B)=\frac{3}{7} $..........(5) 结合(1)(2)(3)(4)(5),可以得到:
$p(AB)=p(A|B)*p(B)=p(B|A)*p(A) $..........(6) 假设下面情形:
已知拿出枪的概率是:
$p(A)=\frac{2}{3} $ 拿出枪以后拿出弹夹的概率
$p(B|A)=\frac{3}{8} $ 拿出弹夹的概率:
$p(B)=\frac{7}{12} $ 求拿出弹夹以后拿出枪的概率
$p(A|B)=\frac{p(B|A)*p(A)}{p(B)} $ 以上就是贝叶斯公式的一般形式,更复杂的形式会在后面的文章中详细介绍。(更复杂的形式是指盒子里有枪,子弹,弹夹,手榴弹。。。。。。)
#数学原理
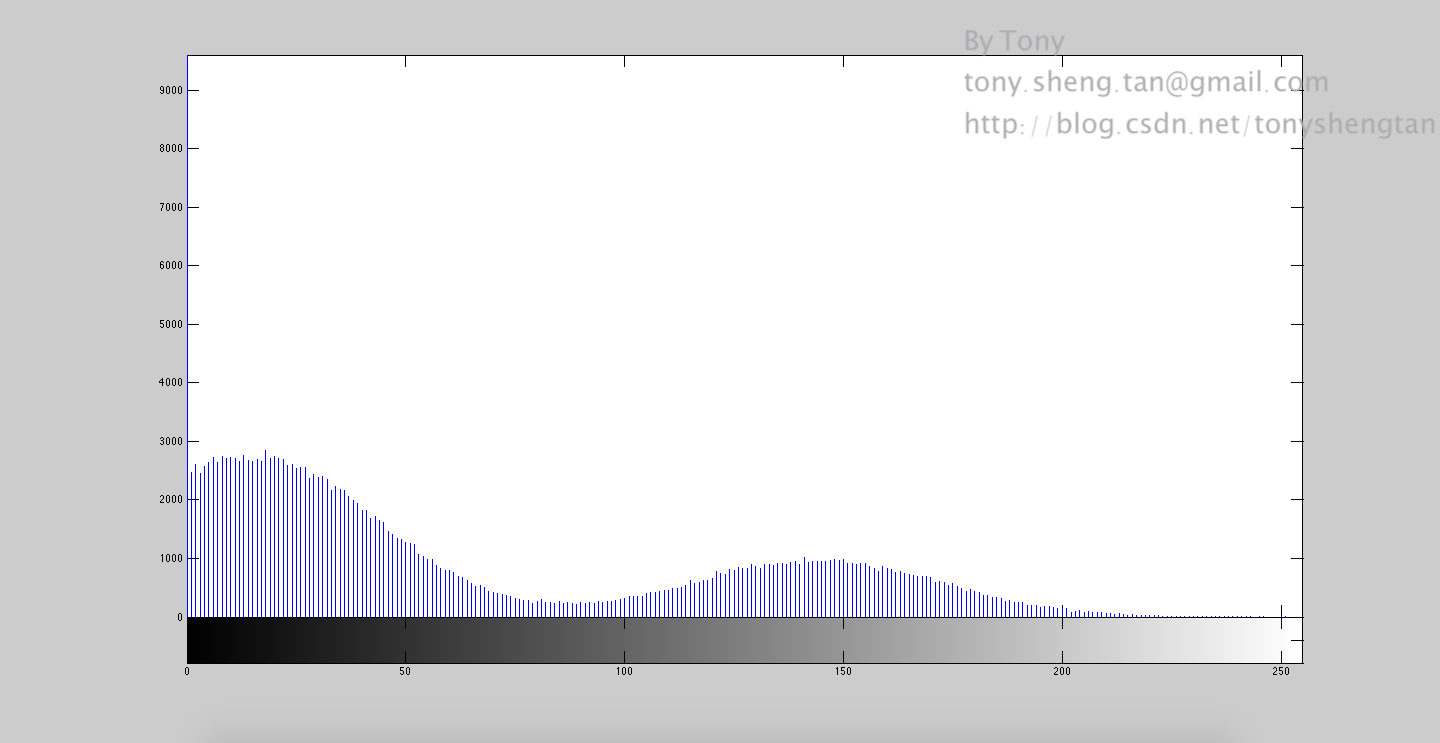
OTSU算法可以基于直方图计算,考虑灰度级为{0,1,2…L-1}大小为$M \times N的 图 像 , 设 的图像,设 的图像,设n_i $为灰度级为i的像素的总数量,那么:
$M \times N=\sum^{L-1}_{i=0}n_i $ $p(n_i)=\frac{n_i}{M \times N} $ $\sum^{L-1}_{i=0}p_i=1 $ 假设阈值为k将直方图分成两部分。
部分1 ( C 1 ) (C_1) (C1?)的概率为:
$p_1(k)=\sum^{k}_{i=0}p_i $ 部分2 ( C 2 ) (C_2) (C2?)的概率为:
$p_2(k)=\sum^{L-1}_{i=k+1}p_i $ 部分1 ( C 1 ) (C_1) (C1?)的平均数:
$m_1(k)=\sum^{k}_{i=0}i*P(i|C_1)=\sum^{k}_{i=0}i*\frac{P(C_1|i)*P(i)}{P(C_1)} $ $P(C_1|i)的 值 为 1 , 因 为 的值为1,因为 的值为1,因为i是 属 于 是属于 是属于C_1的 , 所 以 发 生 的,所以发生 的,所以发生i以 后 发 生 以后发生 以后发生C_1 $的概率是100%,所以
$m_1(k)=\frac{1}{P_1(k)} \sum^{k}_{i=0}i*p_i $ 部分2 ( C 2 ) (C_2) (C2?)的平均数:
$m_2(k)=\frac{1}{P_2(k)} \sum^{L-1}_{k+1}i*p_i $ 全图的均值
$m_G=\sum^{L-1}_{i=0}iP_i $ 上面的式子可以由下面验证:
$P_1m_1+P_2m_2=m_G $ $P_1+P_2=1 $ 下面就是关键部分了,如何评价一个阈值的好坏,提出一个阈值,将像素灰度分为两类,通过以下的公式来评价阈值质量:
$\eta=\frac{\delta_B^2}{\delta_G^2} $ $\delta_G^2=\sum^{L-1}_{i=0}(i-m_G)^2*p_i $ δ B 2 \delta_B^2 δB2?是类间方差,其定义为:
$\delta_B^2=P_1(m_1-m_G)^2+P_2(m_2-m_G)^2 $ 公式还可以写成:
$\delta^2_B=P_1P_2(m_1-m_2)^2=\frac{P_1(m_1-m_G)^2}{1-P_1} $ 于是最佳阈值$k^* $由下面得出:
$\delta^2_B(k^*)=max_{0\leq k \leq L-1}\delta^2_B(k) $ 通过上式可以通过迭代计算出最佳的k值。使用k作为阈值,对图像进行处理。
#代码实现
/*
*OTSU 算法
*otsu 算法使用贝叶斯分类原理得到最好聚类
*
*
*/
//归一化直方图void setHist2One(double *hist_d,double *dst_hist_d){
double sum=0.0;
for(int i=0;
imax_deta){
max_deta_location=i;
max_deta=deta;
}
}
return max_deta_location;
}
void OTSUThreshold(double *src,double *dst,int width,int height,int type){
int hist[GRAY_LEVEL];
double hist_d[GRAY_LEVEL];
setHistogram(src, hist, width, height);
Hist_int2double(hist, hist_d);
setHist2One(hist_d, hist_d);
double threshold=findMaxDeta(hist_d);
Threshold(src, dst, width, height, threshold, type);
} #观察结果
原图:
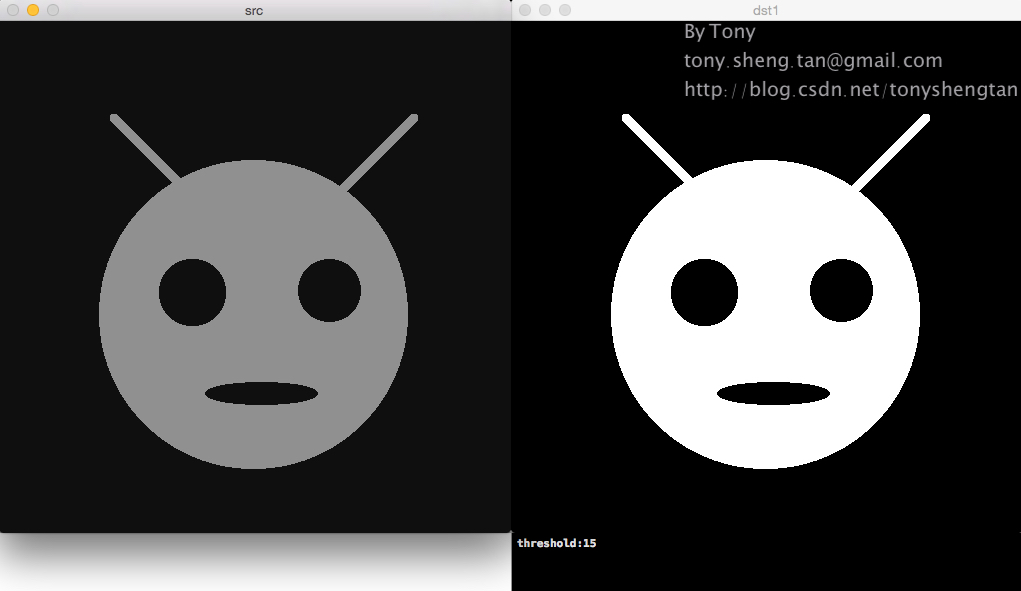 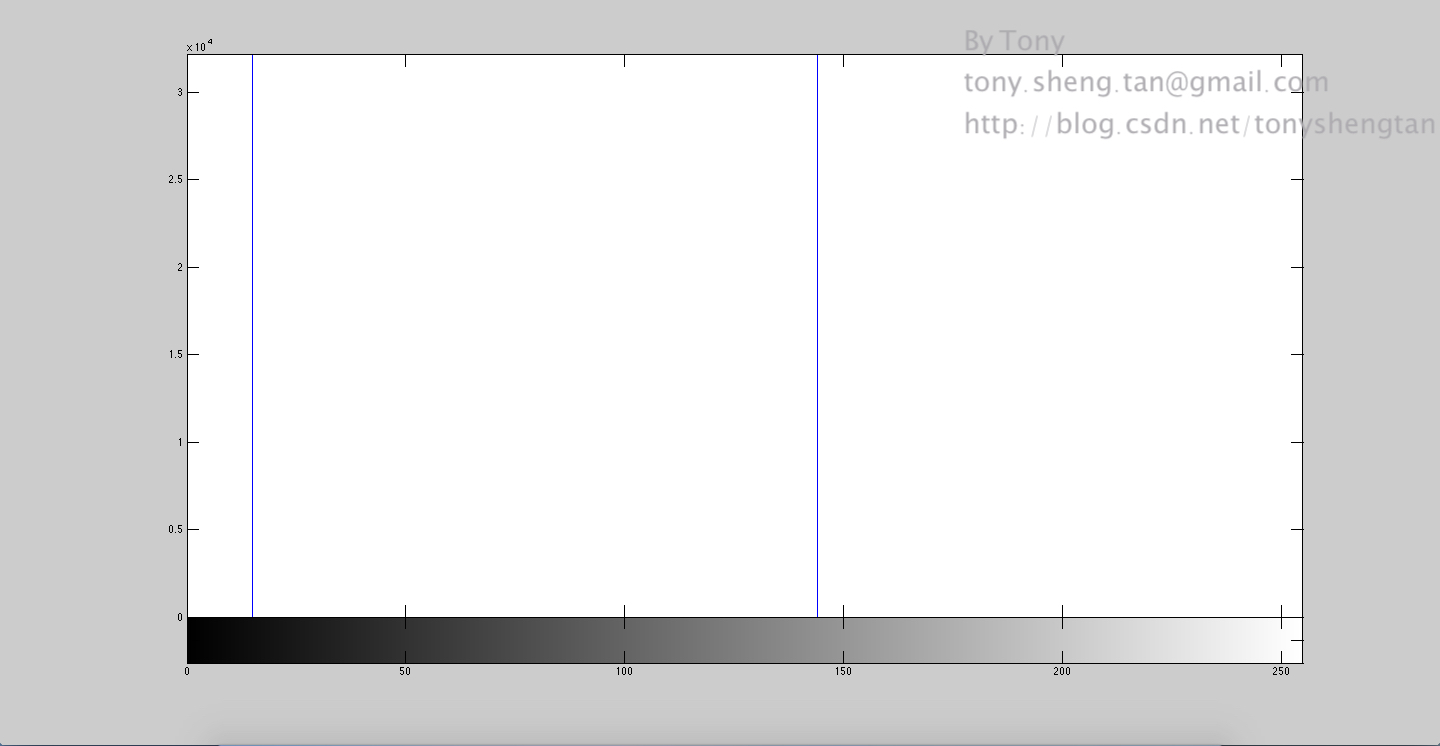 加入1%的高斯噪声:
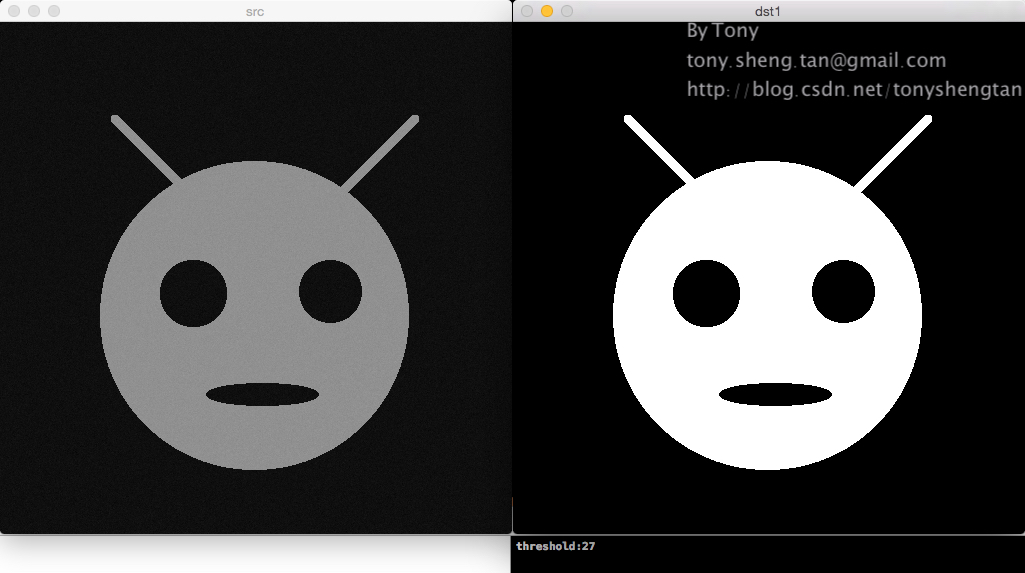 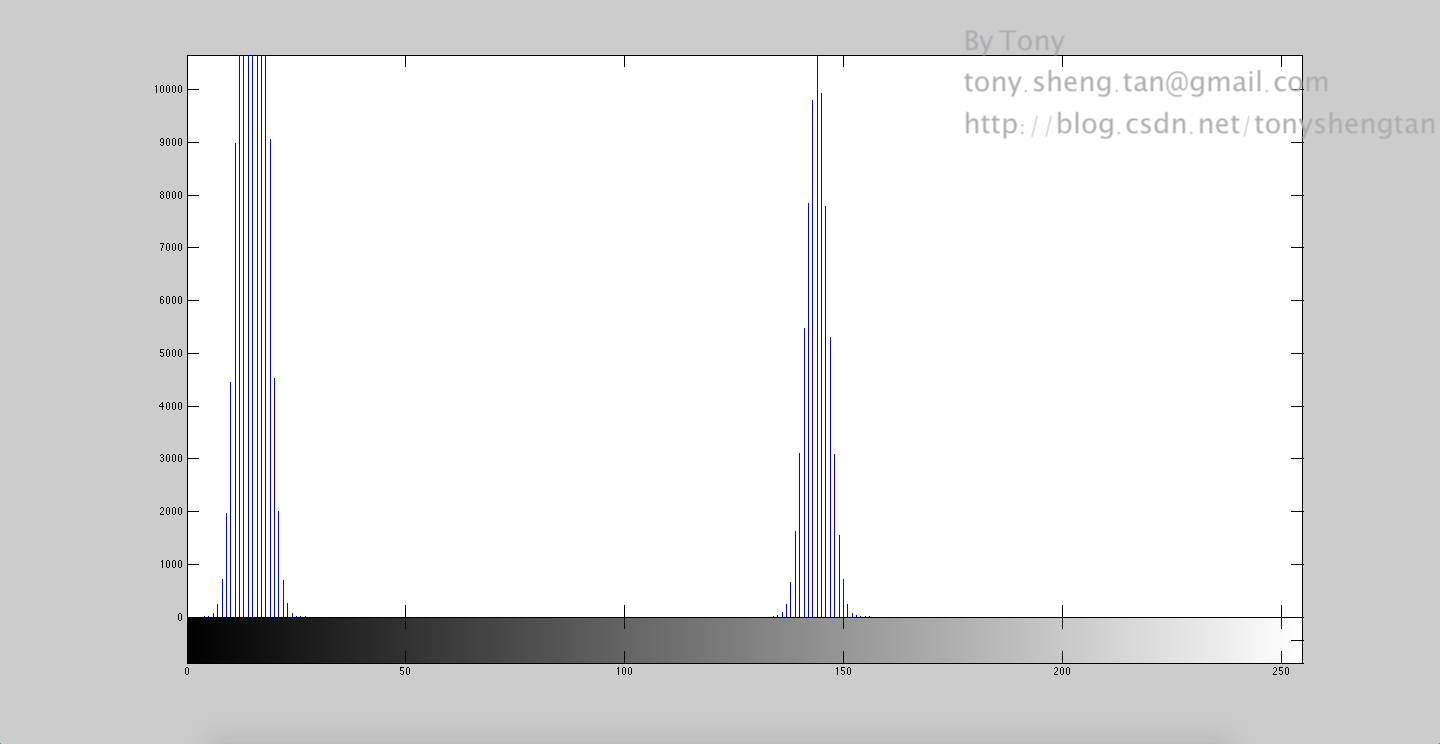 加入3%的高斯噪声:
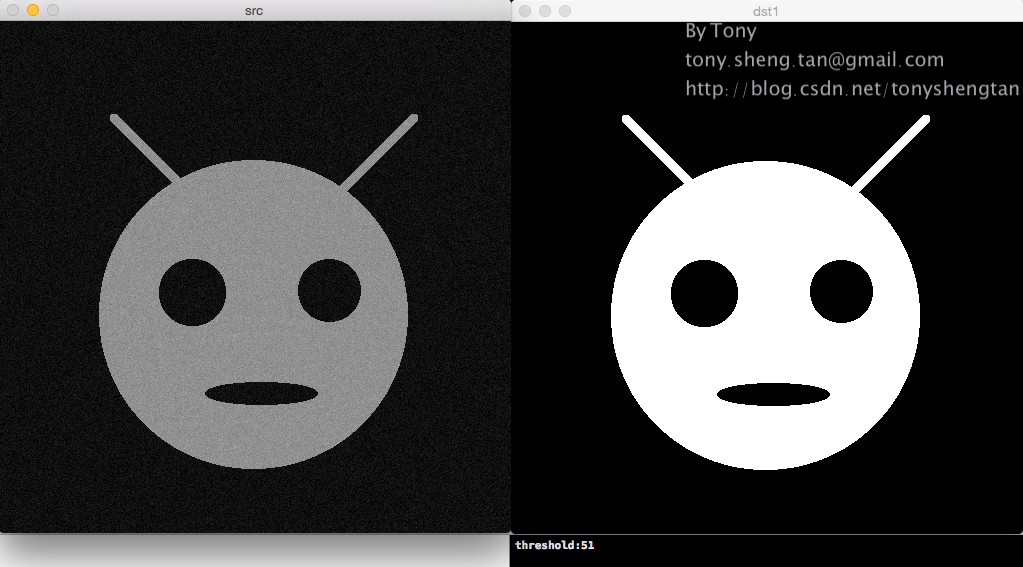 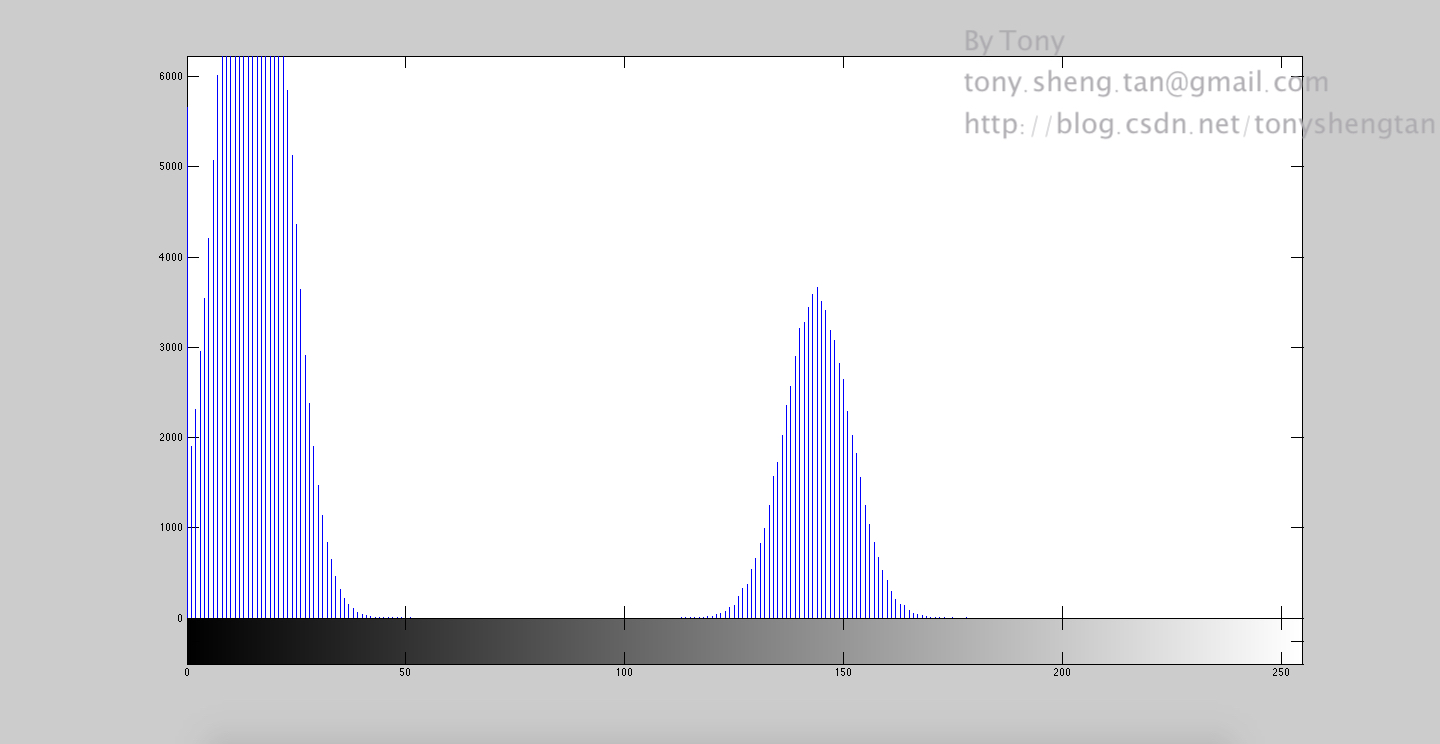 加入5%的高斯噪声:
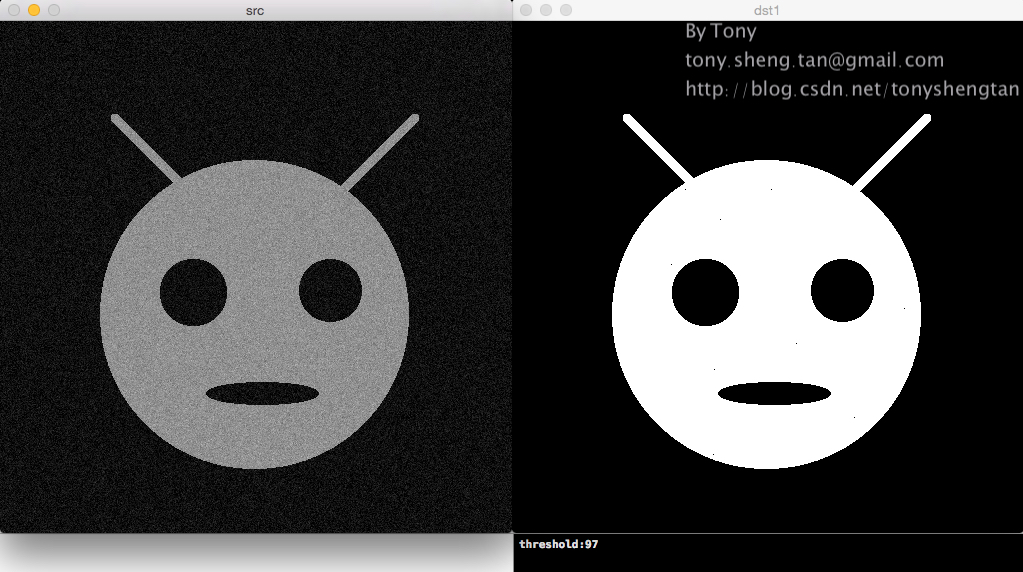 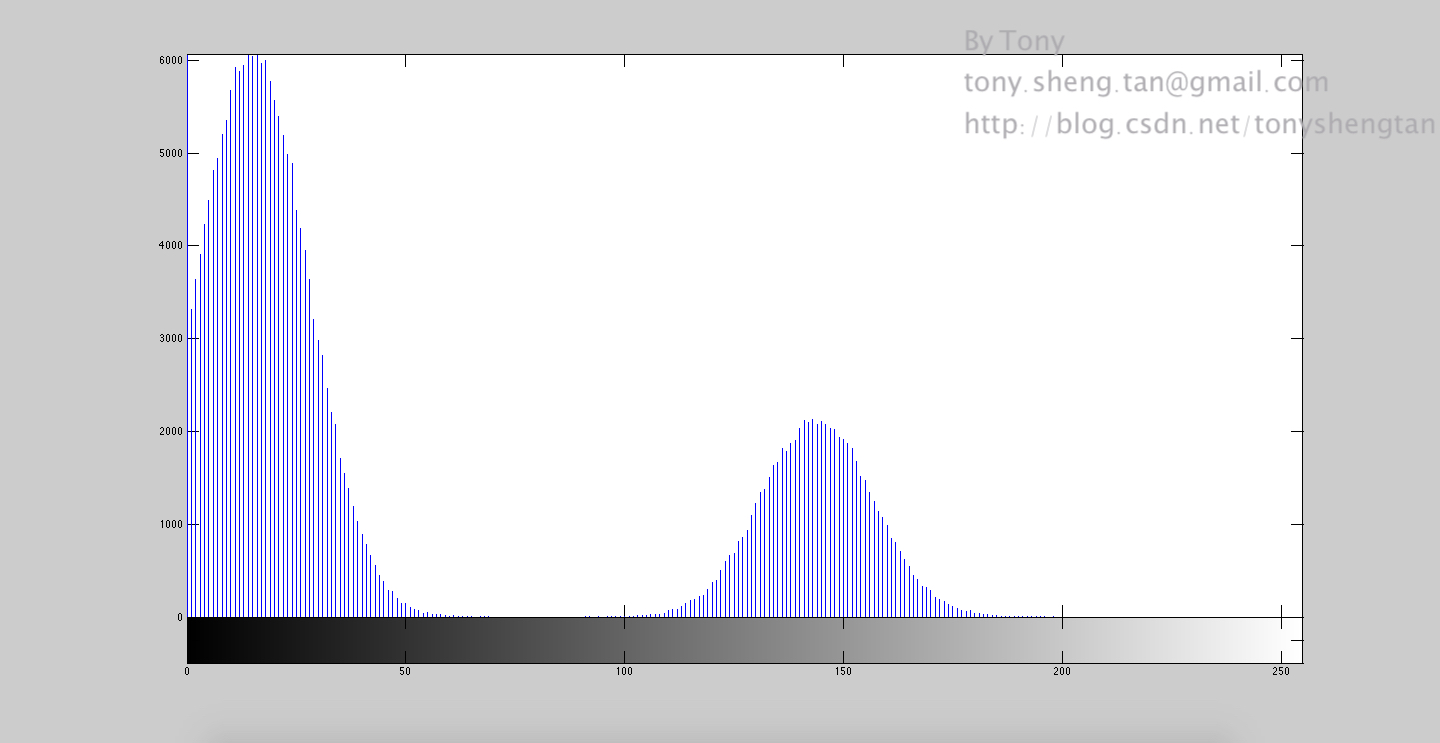 加入7%的高斯噪声:
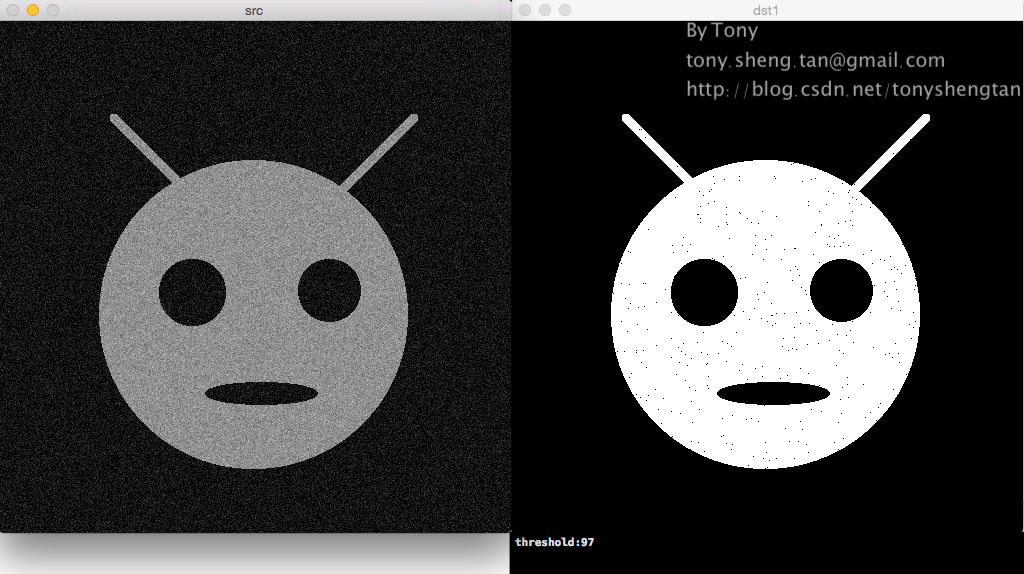 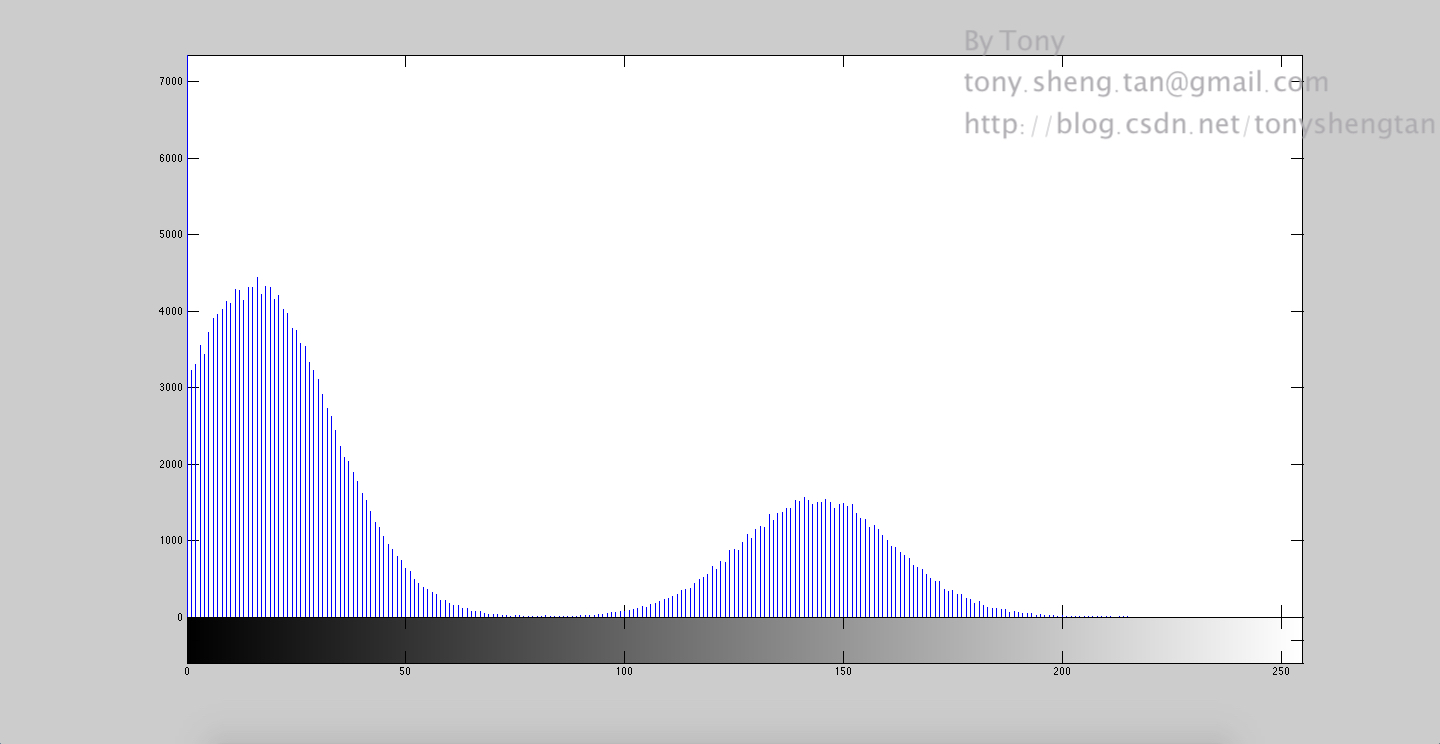 加入9%的高斯噪声:
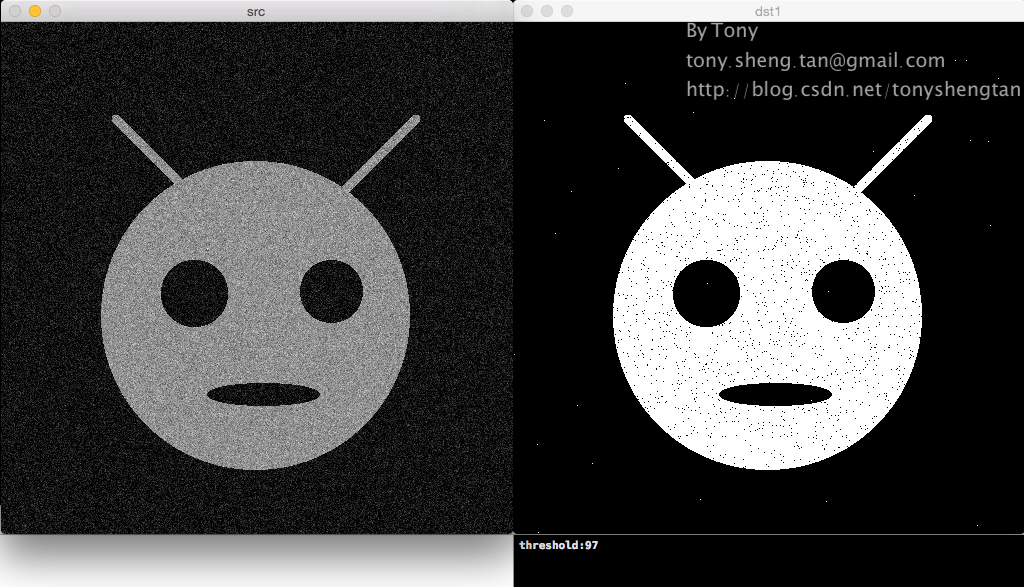 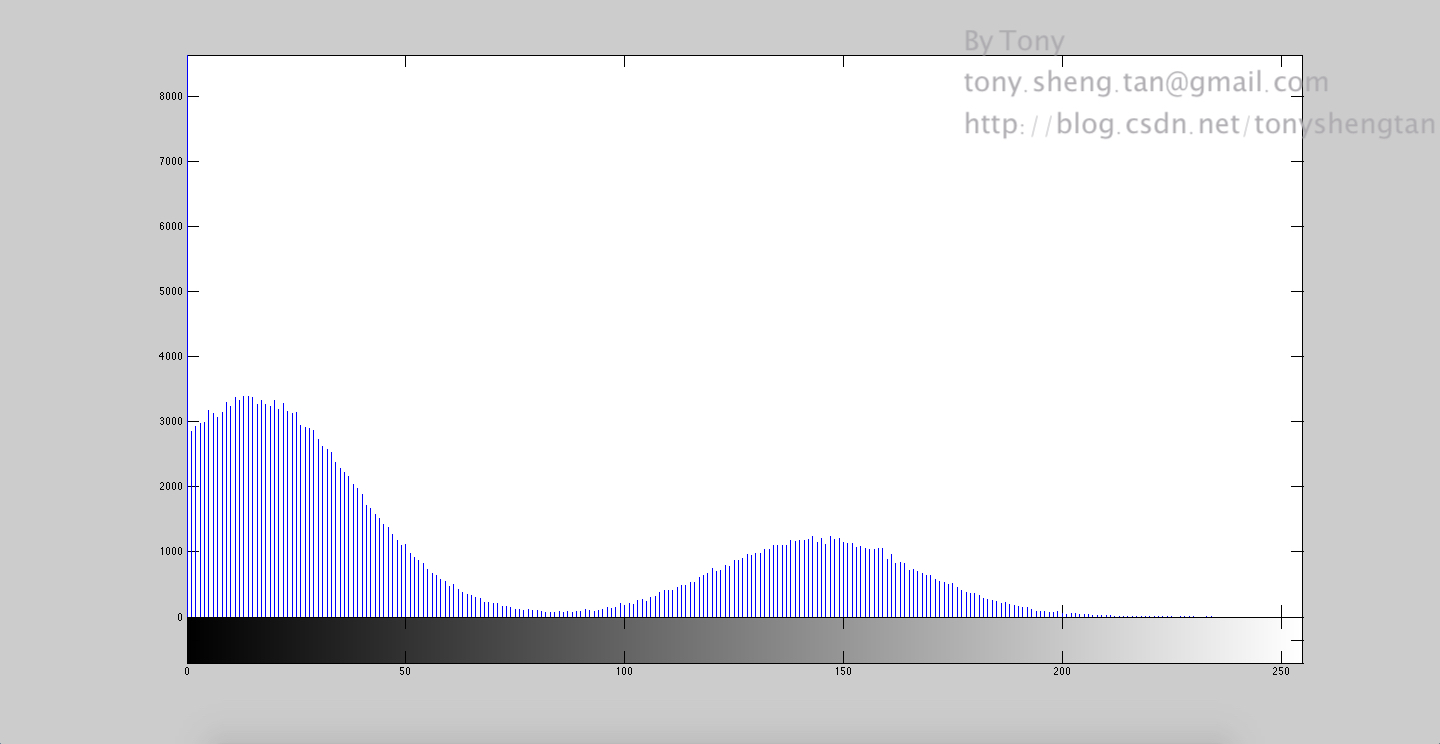 加入11%的高斯噪声:
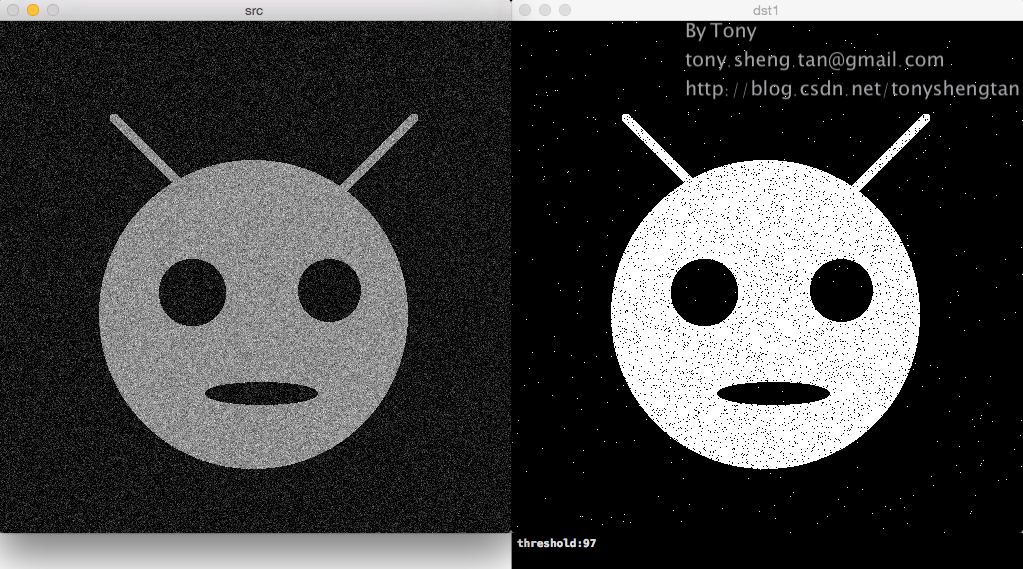  lena:
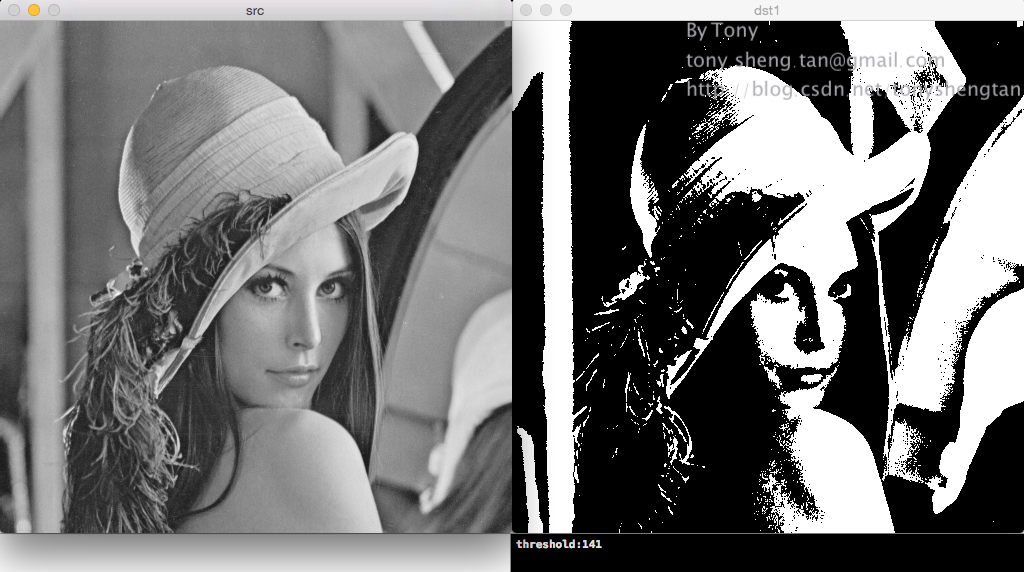 baboon:
 #总结
OTSU算法产生的阈值是数学角度上的最佳分类,数学基础的贝叶斯公式,但应用也有一定的局限性,比如,前面说过最多的,对全局阈值,目标与背景的大小关系,当目标和背景大小相差很多时,或者噪声很大的时候,对OTSU产生影响较大。
待续。。。
更多人工智能机器学习,计算机视觉知识欢迎访问:
理论:
- 数学基础
- 集合论
- 1 样本集
- 2 集合操作
- 分析
- 微积分
- 数学分析
- 《陶哲轩实分析》(包含习题解答)
- 1.0 数学分析介绍
- 2.0 自然数概述
- 2.1 Peano公理
- 2.2 加法
- 2.3 乘法
- 3.0 集合论
- 3.1 集合基础(Part I)
- 3.1 集合基础(Part II)
- 3.2 罗素悖论(选读)
- 3.3 函数(I)
- 3.3 函数(II)
- 《陶哲轩实分析》(包含习题解答)
- 实分析
- 复分析
- 泛函分析
- 测度论
- 线性代数
- 《Introduction to Linear Algebra》
- 线性代数BigPicture
- 1.0 向量
- 1.1 线性组合
- 1.2 点乘和长度
- 2.1 Ax=b
- 2.2 消元
- 2.3 消元和矩阵
- 2.4 矩阵计算
- 2.5 逆
- 2.6 LU和LDU分解
- 2.7 映射与排列
- 3.1 向量空间
- 3.2 Null 空间
- 3.3 秩
- 3.4 Ax=B
- 3.5 线性独立,基和维度
- 3.6 四个空间的维度
- 4.1 四个子空间的正交
- 4.2 投影
- 4.3 最小二乘(略)
- 4.4 正交基和Gram-Schmidt算法
- 5.1 行列式的性质
- 5.2 排列和代数余子式
- 5.3 Cramer’s 法则,逆和体积
- 6.1 特征值介绍
- 6.2 矩阵对角化
- 6.3 微分方程应用(略)
- 6.4 对称矩阵
- 6.5 正定矩阵
- 6.6 相似矩阵
- 6.7 奇异值分解
- 7.1 线性变换思想
- 7.2 线性变换的矩阵
- 7.3 对角化和伪逆
- 《Introduction to Linear Algebra》
- 微分方程
- 拓扑学
- 概率论
- 概率论BigPicture
- 1.0 概率介绍、试验、事件、公理化的概率
- 1.1 样本空间、柯氏公理、概率的性质
- 1.2 古典概率、乘法原理、排列
- 1.3 组合、二项式定理、多项式定理
- 1.4 有限事件并的概率、概率欺骗了你
- 2.1 条件概率、全概率公式
- 2.2 事件独立、条件独立
- 2.3 Bayes’ Theorem
- 3.1 随机变量和离散分布
- 3.2 连续分布
- 3.3 Cumulative Distribution Function
- 3.4 双变量分布
- 3.5 边缘分布不和独立随机变量
- 3.6 条件分布 (Part I)
- 3.6 条件分布 (Part II)
- 3.7 多变量分布(Part I)
- 3.7 多变量分布(Part II)
- 3.8 随机变量的函数
- 3.9 多随机变量的函数
- 4.1 随机变量的期望 (Part I)
- 4.1 随机变量的期望 (Part II)
- 4.2 期望的性质
- 4.3 方差
- 4.4 距
- 4.5 均值和中值
- 4.6 协方差和相关性
- 4.7 条件期望
- 5.1 分布介绍
- 5.2 伯努利和二项分布
- 5.3 超几何分布
- 5.4 泊松分布
- 5.5 负二项分布
- 5.6 正态分布(Part I)
- 5.6 正态分布(Part II)
- 5.6 正态分布(Part III)
- 5.7 Gamma分布(Part I)
- 5.7 Gamma分布(Part II)
- 5.8 Beta分布
- 5.9 多项式分布
- 5.10 二维正态分布
- 6.1 大样本介绍
- 6.2 大数定理
- 6.3 中心极限定理
- 6.4 连续性修正
- 数理统计
- 《数理统计学简史》
- 介绍
- 早期概率论——从萌芽到《推测术》
- 1.1 卡丹诺的著作
- 1.2 分赌本问题
- 1.3 帕斯卡和费马的通信
- 1.4 惠更斯的“机遇与规律”
- 1.5 《推测术》前三部分内容提要
- 1.6 关于概率的几点看法
- 1.7 伯努利大数定律
- 2.0 狄莫弗的二项概率逼近
- 2.1 狄莫弗研究的动因
- 2.2 狄莫弗的初步结果
- 2.3 初步结果的改进,与斯特林的联系
- 《数理统计学简史》
- 随机过程
- 信息论
- 凸优化
- 集合论
- 算法设计过程
- 算法
- 机器学习算法
- 统计学习算法
- 深度学习算法
- FaceNet论文阅读
- 可视化CNN
- LeNet
- Dropout
- CNN训练数据选择
- 图像处理
- 1.1 灰度级
- 1.2 灰度变换,gama变换,对数,反对数变换
- 2.1 一维DFT
- 2.2 二维DFT
- 2.3 FFT算法理解与c语言的实现
- 2.4 二维FFT,IFFT,c语言实现
- 2.5 图像傅里叶变换(快速傅里叶变换FFT)
- 3.0 二值图像
- 3.1 二值图像-形态学处理 数学形态学
- 3.2 二值图像-形态学处理 腐蚀和膨胀
- 3.3 二值图像-形态学处理 开操作和闭操作
- 3.4 二值图像-形态学处理4 其他操作
- 4.0 灰度图像
- 4.1 灰度图像-形态学处理
- 4.2 灰度图像-频域滤波 傅里叶变换之卷积
- 4.3 灰度图像-频域滤波 傅里叶变换之连续周期信号傅里叶级数
- 4.4 灰度图像-频域滤波 傅里叶变换之离散周期信号傅里叶级数
- 4.5 灰度图像-频域滤波 傅里叶变换之连续信号傅里叶变换(FT)
- 4.6 灰度图像-频域滤波 傅里叶变换之采样定理
- 4.7 灰度图像-频域滤波 傅里叶变换之离散时间傅里叶变换(DTFT)
- 4.8 灰度图像-频域滤波 傅里叶变换之离散傅里叶变换(DFT)
- 4.9 灰度图像-频域滤波 傅里叶变换之二维离散傅里叶变换
- 4.10 灰度图像-频域滤波 概论
- 4.11 灰度图像-频域滤波 滤波器
- 4.12 灰度图像-频域滤波 同态滤波
- 5.0 灰度图像-空域滤波 基础:卷积和相关
- 5.1 灰度图像-图像增强 综合介绍
- 5.2 灰度图像-图像增强 平滑之均值滤波、高斯滤波
- 5.3 灰度图像-图像增强 双边滤波 Bilateral Filtering
- 5.4 灰度图像-图像增强 中值滤波
- 5.5 灰度图像-图像增强 锐化基础
- 5.6 灰度图像–图像增强 拉普拉斯算子
- 5.7 灰度图像-图像增强 非锐化掩蔽 (Unsharpening Mask)
- 5.8 灰度图像-图像增强 Robert算子、Sobel算子
- 5.9 灰度图像–图像增强 灰度变换
- 5.10 灰度图像–图像增强 直方图均衡化(Histogram Equalization)
- 5.11 灰度图像-图像增强 直方图匹配(规定化)Histogram Specification
- 6.0 灰度图像-图像分割 综合介绍
- 6.1 灰度图像-图像分割 边缘模型
- 6.2 灰度图像-图像分割 边缘检测算子 综述
- 6.3 灰度图像-图像分割 Robert算子
- 6.4 灰度图像-图像分割 Sobel算子
- 6.5 灰度图像-图像分割 Prewitt算子
- 6.6 灰度图像-图像分割 Scharr算子
- 6.7 灰度图像-图像分割 Sobel算子,Prewitt算子和Scharr算子平滑能力比较
- 6.8 灰度图像-图像分割 Canny边缘检测
- 6.9 灰度图像-图像分割 Marr-Hildreth算子(LoG算子)
- 6.10 灰度图像-图像分割 霍夫变换(Hough Transform)–直线
- 7.0 灰度图像-图像分割 阈值处理综述
- 7.1 灰度图像-图像分割 阈值处理之平均阈值
- 7.2 灰度图像-图像分割 阈值处理之P-Tile阈值
- 7.3 灰度图像–图像分割 阈值处理之迭代均值阈值
- 7.4 灰度图像-图像分割 阈值处理之谷底阈值、峰顶平均
- 7.5 灰度图像-图像分割 阈值处理之OTSU阈值
- 7.6 灰度图像–图像分割 阈值处理之补充说明
- 7.7 灰度图像-图像分割 阈值处理之局部阈值
- 7.8 灰度图像-图像分割 区域分割之区域生长
- 7.9 灰度图像-图像分割 区域分割之区域分离
- 7.10 灰度图像-图像分割 区域分割之分水岭算法
- 8.0 彩色模型,CIE XYZ,CIE RGB
- 8.1 彩色图像-色彩空间 综述
- 8.2 彩色图像-色彩空间 RGB系列
- 8.3 彩色图像-色彩空间 CMY(K)空间
- 8.4 彩色图像-色彩空间 YIQ 、YUV 、YCbCr 、YC1C2 和I1I2I3
- 8.5 彩色图像-色彩空间 CIELAB、CIELUV
- 8.6 彩色图像-色彩空间 HSI(HSL)、HSV(HSB)
- 8.7 彩色图像-色彩空间 总结
- 9.1 彩色图像-伪彩处理 灰度图转伪彩色图像
- 9.2 彩色图像-彩色变换 补色处理
- 10.1 彩色图像-图像增强 直方图增强
- 10.2 彩色图像-图像增强 图像平滑
- 10.3 彩色图像-图像增强 图像锐化
- 10.4 彩色图像-图像分割 彩色空间分割
- 遗传算法
- 机器学习算法
- 神经生物学
技术
- 语言
- C++
- Python
- Web Crawler
- 1.0 Introduction
- 2.0 分析目标网站
- 3.0 三只虫
- 3.1 HTTP协议(一)
- 3.2 HTTP协议(二)
- 3.3 数据抓取
- Web Crawler
- CUDA
- 0.0 腾讯云CUDA环境搭建
- 1.0 并行计算与计算机架构
- 1.1 异构计算与CUDA
- 2.0 CUDA编程模型概述(一)
- 2.1 CUDA编程模型概述(二)
- 2.2 给核函数计时
- 2.3 组织并行线程
- 2.4 设备信息查询
- 3.1 CUDA执行模型概述
- 3.2 理解线程束执行的本质(Part I)
- 3.2 理解线程束执行的本质(Part II)
- 3.3 并行性表现
- 3.4 避免分支分化
- 3.5 循环展开
- 3.6 动态并行
- 4.0 全局内存
- 4.1 内存模型概述
- 4.2 内存管理
- 4.3 内存访问模式
- 4.4 核函数可达到的带宽
- 4.5 使用统一内存的向量加法
- 框架
- OpenCV
- OpenCV矩阵计算分析
- TensorFlow .etc
- OpenCV
- 设计实现框架
- PineNut
【数字图像处理|灰度图像--图像分割 阈值处理之OTSU阈值】随笔
- 其他
- 推荐读物
- 学习
- Hexo博客搭建
- Hexo畅言评论PC和移动端同步
推荐阅读
- 图像处理|OpenCV Tutorials(三)矩阵的掩码(或卷积)操作
- 日常小技巧|任意角度旋转图片(python)
- 算法|2021APMCM赛后总结——边缘检测
- matlab图像处理|matlab-图形采样及灰度级转换
- OpenCV|OpenCV-图像锐化
- 技术交流|详解用OpenCV绘制各类几何图形
- 数字图像处理|数字图像处理5(图像金字塔)
- 图像处理|5分钟学会,使用opencv进行基本的图像操作—读、写、显示、缩放、裁剪(python语言)
- 计算机视觉|Opencv 基于C++识别绿灯













